From this fall, my son will start 11th grade in a MINT school in Berlin. MINT stands for Mathematik, Informatik, Naturwissenschaften und Technik (Math, Computer Science, Natural Science, and Technology). He now enjoys these scientific subjects, but he used to get confused in math, starting with the differences in the German and Japanese counting systems at elementary school. Since he was taking a monthly Japanese correspondence course and was in the Japanese supplementary school in Berlin to be a balanced bilingual, the confusion intensified. As his math classes progressed, more differences between Japanese and German math education became apparent. I will introduce some of these differences in this article.
Differences in reading numbers
He encountered the first hurdle in a local elementary school in Berlin, when two-digit numbers were introduced in math class. Until then, he had been solving calculation problems smoothly, but suddenly, he started to leave a lot of blank spaces in his assignments. When I talked to him carefully to understand what was going on, I discovered that the problem lay in how he read two-digit numbers.
For example, in Japanese and English, the number "21" is read from left to right as ni-juu (twenty)" and ichi (one), making ni-juu-ichi (twenty-one). However, in German, it is the opposite; "21" is read as Ein (1) and Zwanzig (20), making Ein und Zwanzig (one and twenty). Therefore, he got confused with certain two-digit numbers, such as "12" and "21," or "23" and "32," which affected his calculation problems.
The Japanese supplementary school he attended weekly recognized this difference and had been giving training on counting in Japanese for over six months. Thanks to this, he mastered the Japanese way of reading numbers. However, he then seemed to get confused with the German way of reading numbers.
In fact, I myself still haven't gotten used to this difference, and I often have to check the monitor at the register when shopping to see how much I need to pay. Fortunately, after that, my son received intensive training from his German father on how to count in German for several days, and it seems he has gotten over this confusion.
Differences in writing numbers
Our son has been attending the Japanese supplementary school once a week to maintain his Japanese ability. This school conducts the Kanji Aptitude Test twice a year. (Kanji are the logographic Chinese characters used in Japanese writing.) Prior to the test, special classes were held to prepare the students, mainly focusing on past exam questions. This led to a small problem when he was in the first grade.
The Kanji Aptitude Test at level 10 includes questions about the stroke order of kanji characters, because the stroke order is considered to be important in kanji learning. The answers are to be written in numbers. However, my son's answers, written in the German style, were marked incorrect. This is because they were "not written in the Japanese style" and therefore, difficult for the graders in Japan to read, even though his answers were correct.
The specific numbers that were pointed out were 1, 7, and 9, as shown in the photo.
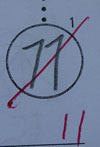 |
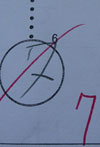 |
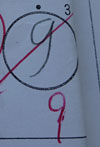 |
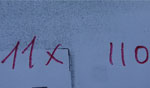 |
 |
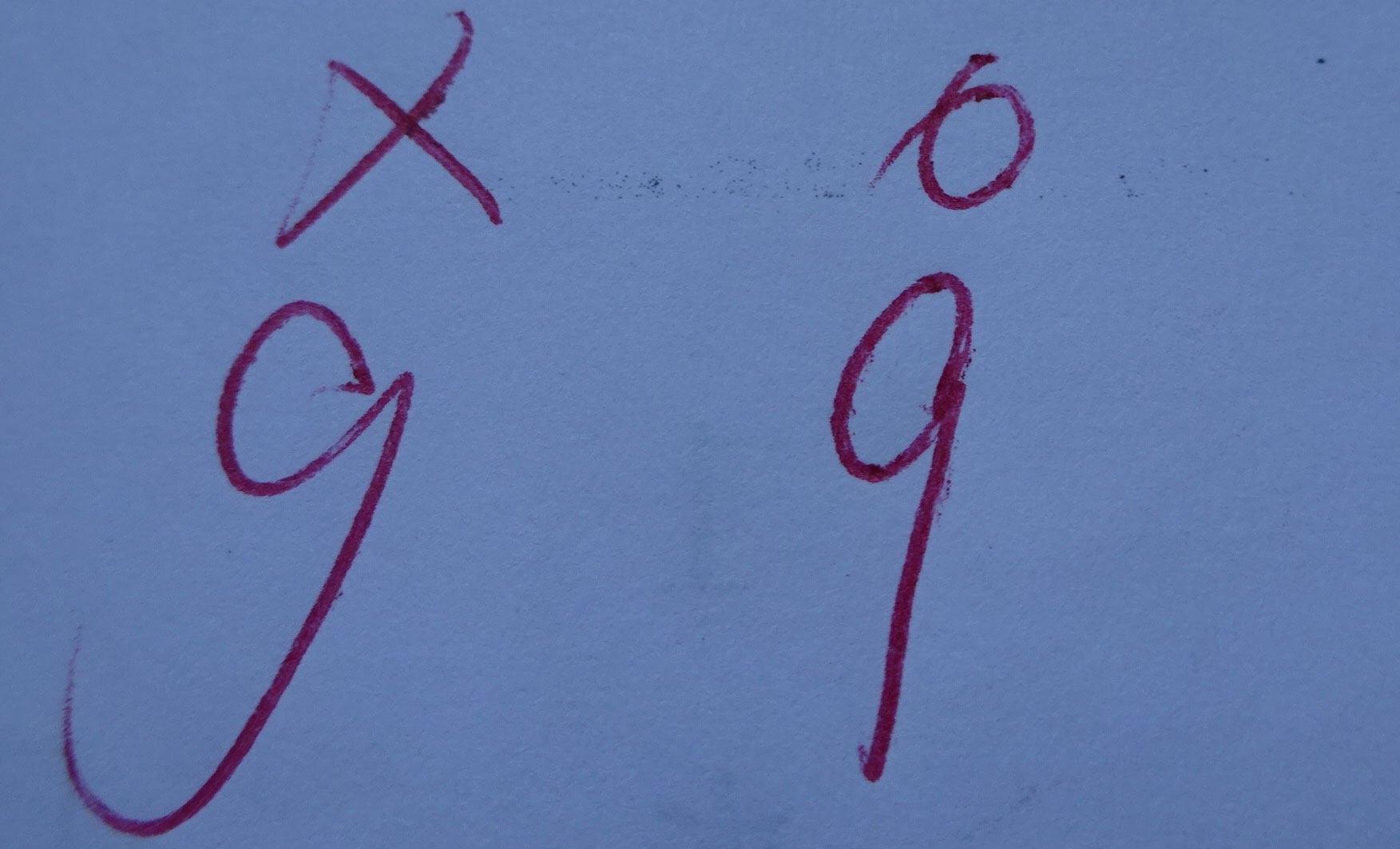 |
Although my son had math classes at the Japanese supplementary school in first grade, he didn't learn the Japanese way of writing numbers. This was pointed out for the first time during the Kanji Aptitude Test preparation, which left my son somewhat shocked. Initially, he was frustrated, saying, "Why is it wrong when the answer is correct?!" However, if the Japanese graders for the Kanji aptitude test cannot read his answers, it will be meaningless. It seems that the Japanese supplementary school took this opportunity to thoroughly teach the Japanese way of writing numbers. I also explained at home the importance of writing in a way that the readers can understand.
However, if he wrote numbers in the Japanese style at his German local school, he might be corrected as was the case at the supplementary school. My son learned the importance of changing the way he writes numbers depending on the situation through the Kanji Aptitude Test preparation.
No Memorization of Multiplication Tables in Germany
In his second grade, multiplication was introduced in the local elementary school. When I was a child, multiplication meant memorizing the multiplication table (ku-ku) like a chant: "Two times two is four (ninin-ga-shi), two times three is six (nisan-ga-roku)...." This is the first step to mental arithmetic.
In Germany, there is no need to memorize such "chants." For example, "two times two" is said as "Zwei mal Zwei ist gleich Vier" (which translates to "two times two equals four") and "two times three" as "Zwei mal Drei ist gleich Sechs" (two times three equals six) in a normal sentence.
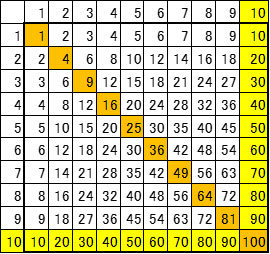
Moreover, while the multiplication table goes up to nine in Japan, it goes up to ten in Germany. The following multiplication table is distributed, and children initially solve multiplication problems by referring to it.
 |
 |
||
| Left: Multiplication table used in German elementary schools (squares highlighted) Right: Multiplication table (ku-ku) used in Japanese elementary schools |
|||
This elementary school did not use any textbooks for math but only workbooks, and the class progressed at each student's own pace. The workbook contained problems to complete the table, problems to learn the concept of multiplication through illustrations, simple calculation problems, and word problems.
Interestingly, the concept of squares was also taught in second grade, with the squares of each number on the multiplication table highlighted in different colors, and these squares repeatedly appear in the workbook as "2×2", "3×3", "4×4"....
Moreover, in Japan, "2×2=4" is written using "×" , but in Germany, it is written as "2·2=4" using the "·". The division symbol is also different; Japanese division "4÷2=2" is written as "4:2=2" using the ":" symbol in Germany.
Learning Multiplication and Division Simultaneously
In the elementary school that my son attended, multiplication and division were taught together. This is another point of difference in Japanese and German math education, because in Japan, we learn these calculations separately, first multiplication and then division.
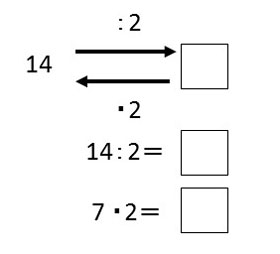
While he was working with two-digit numbers calculation, he had a great many questions as below in the workbook to fill in the box.
 |
|
I was actually impressed by the rationality of the German method of introducing multiplication and division simultaneously. It seems to make calculations easier to understand if the relationships between numbers are learned in this way.
Soon after, they also learned division with remainders, solving many problems such as "23:3=7 Rest 2 (23÷3=7 remainder 2)". At the same time, they solved reverse problems like "7×3+2=23". After practicing calculations, they also worked on word problems.
Different Methods for Longhand arithmetic
As mentioned above, my son used to take a monthly Japanese correspondence course including math. His grandparents in Japan sent these materials to him in Germany. One day, he was puzzled when he started learning addition and subtraction with carrying and borrowing. This was because he had never written calculations vertically in his German school until then.
In German-style addition, even with carry-up, it's written horizontally like "13+28=41". My son used to calculate it in three steps: "3+8 is 11. 10+20 is 30. 11+30 is 41". However, I personally, think vertical calculation is easier for carrying and borrowing, so I took the time to teach my son. He found that vertical calculation was indeed easier and managed to solve problems that way.
Regarding subtraction with borrowing, they do use vertical calculation in Germany, but it seems a little different from the Japanese way.
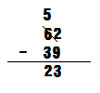
For example, the problem 62-39 would be solved in Japanese vertical subtraction as follows:
 |
|
We can't subtract 9 from 2, so we borrow 1 from the tens column to make it "12-9=3". Then, the digit in the tens column becomes "5", so "5-3=2", resulting in 23.
On the other hand, German vertical subtraction looks like this:
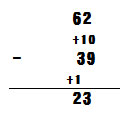 |
|
When I first saw this, I had no idea what it meant and had to ask my German husband. His explanation was as follows:
Since you can't subtract 9 from 2, you add 10 to 2 to make "12-9=3."
Then you add 1 to the tens column of 39, because you borrowed 1 from the tens column of 62, making the tens "6-(3+1)=2". Therefore, the answer is 23.
The calculation for the ones column is the same as the Japanese method, but the one for the tens column is different. In the Japanese method, the number being subtracted is decreased, while in the German method, the subtracting number is increased. The result is the same, but the calculation process is totally different.
So far, I have described the differences in calculation methods and number notation between Japan and Germany. These differences may confuse children. Therefore, the Japanese supplementary school decided to eliminate math classes in order to avoid confusion.
As for our son, I gave him some additional math workbooks for vertical calculation and let him solve the problems in either way as long as the answer was correct.
The Underlying Philosophy of Math Education in Germany
Lastly, the most surprising aspect of math education in Germany is the widespread belief that "calculations are more efficiently done by using calculators." From middle school onwards, students are allowed to use calculators not only in classes but also in exams. Therefore, teaching the concepts of numbers and formulas at a young age is considered important, but the calculations themselves are not emphasized as much as in Japan. In Japanese elementary schools, arithmetic drills are assigned as homework every day, and it seems that the children's calculation skills are steadily improving.
My German husband says, "Calculators are more accurate and faster. Even when I was a child, calculations were not that important. In the real world, Excel is better at formulas. Humans should do what computers can't."
On the other hand, the schools seem to emphasize understanding the concepts of numbers and the calculation process. This helps students to develop the logical thinking skills necessary for explaining things logically in real-life situations.
Conclusion
I think it is important to develop logical thinking at school. When looking at the math assignments from local schools in Berlin, I found a great many word problems from early grades. However, having grown up in Japan, I can't help but think that it is convenient to be able to do mental arithmetic in the real world, such as in shopping and business. Then, I thought "why not develop both skills at the same time?" So, I put up a poster of the Japanese multiplication table on the wall in our child's room. He chanted the table repeatedly then and kept taking the Japanese correspondence course until the 6th grade.
Time flies and he will be an 11th grader soon. The other day, I asked him about these differences between Japanese and German math, including calculations and longhand arithmetic, which method was actually easier for him. His answer was, "I used to do calculations in the Japanese way, but since the 9th grade, all calculations have been done using a calculator and computer, so now it doesn't matter." Now I just hope that he has developed both skills!














